All India Pre-Medical/Pre-Dental Entrance Examination (AIPMT) 2009 Questions on Rotational Motion and Centre of Mass

A few questions on circular motion and rotation, which appeared in AIPMT 2011 question paper were discussed in the last post. A few more questions on rotational motion and centre of mass with their solution are given below. These questions were included in the All India Pre-Medical/Pre-Dental Entrance Examination (Preliminary) 2009 question paper:

(1) A thin circular ring of mass M and radius R is rotating in a horizontal plane about an axis perpendicular to its plane with a constant angular velocity ω. If two objects each of mass m be attached gently to the opposite ends of a diameter of the ring, the ring will then rotate with an angular velocity

(1) ωM /(M + 2m)

(2) ω(M + 2m) /M

(3) ωM /(M + m)

(4) ω(M – 2m) /(M + 2m)

This question is a popular one and has appeared in various entrance question papers. Its answer is based on the law of conservation of angular momentum:

I₁ω₁ = I₂ω₂ where I₁ and I₂ are the initial and final moments of inertia and ω₁ and ω₂ are the initial and final angular velocities respectively.

Therefore we have

MR²ω = (MR² + 2 mR²) ω₂

Therefore, ω₂ = ωM /(M + 2m)

(2) Four identical thin rods each of mass M and length L, form a square frame. Moment of inertia of this frame about an axis through the centre of the square and perpendicular to its plane is

(1) (²/₃) ML²

(2) (¹³/₃) ML²

(3) (¹/₈) ML²

(4) (⁴/₃) ML²

We have to use the theorem of parallel axes: I = I_CM + Ma² where I_CM is the the moment of inertia about an axis through the centre of mass of the rod and I is the moment of inertia about a parallel axis at distance a.

The moment of inertia of a thin rod of mass M and length L about an axis through the mid point of the rod and perpendicular to its length is ML²/12. The moment of inertia of the rod about a parallel axis at a distance L/2 (which is the distance of the centre of the frame from each ro.is ML²/12 + M (L/2)² = ML²/3

You must remember that moment of inertia is a scalar quantity. Since there are four rods in the square frame, the moment of inertia of the entire frame is four times the moment of inertia of one rod. Therefore the answer is (⁴/₃) ML²

(3) If F is the force acting on a particle having position vector r and τ be the torque of this force about the origin, then

(1) r.τ > 0 and F.τ < 0

(2) r.τ = 0 and F.τ = 0

(3) r.τ = 0 and F.τ ≠ 0

(4) r.τ ≠ 0 and F.τ = 0

This question may appear to be a difficult one at the first glance. But this is a very simple question if you remember that the torque τ is the ‘cross product’ (vector product) of r and F:

τ = r×F

The ‘cross product’ of two vectors is a vector perpendicular to both individual vectors. The torque vector is thus perpendicular to both r and F. Therefore the ‘dot product’ (scalar product) of r and τ as well as that of F and τ is zero [Option (2)].

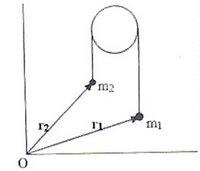
(4) Two bodies of mass 1 kg and 3 kg have position vectors i + 2 j + k and –3 i – 2 j + k espectively. The centre of mass of this system has a position vector

(1) –2 i – j + k

(2) 2 i – j – 2 k

(3) – i + j + k

(4) –2 i + 2 k

If two point masses m₁ and m₂ have position vectors r₁ and r₂ their centre of mass has position vector R given by

R = (m₁ r₁ + m₂ r₂) /( m₁ + m₂)

Here we have m₁ = 1, m₂ = 3, r₁ = i + 2 j + k and r₂ = –3 i – 2 j + k

Substituting, R = [1(i + 2 j + k) + 3(–3 i – 2 j + k)] /(1+3)

Or, R = (– 8 i – 4 j + 4 k) /4 = –2 i – j + k

You can access all questions in this section by clicking on the label ‘rotation’ below this post. Make use of the buttons ‘older posts’ and ‘newer posts’ at the end of the page to navigate through all the posts.

All India Pre-Medical/Pre-Dental Entrance Examination (Preliminary) 2010 (AIPMT 2010) Multiple Choice Questions on Centre of Mass

The following questions (MCQ) on centre of mass were included in the AIPMT 2010 question paper:

(1) A man of 50 kg mass is standing in a gravity free space at a height of 10 m above the floor. He throws a stone of 0.5 kg mass downwards with a speed 2 ms^–1. When the stone reaches the floor, the distance of the man above the floor will be

(1) 20 m

(2) 9.9 m

(3) 10.1 m

(4) 10 m

You can work out this question either by using the concept of centre of mass or by applying the law of conservation of momentum.

The position of the centre of mass of the man-stone system will be unchanged as there are no external forces. If x is the distance of the man from the centre of mass when the stone reaches the floor, we have

50×x = 0.5×10 from which x = 0.1 m

As the centre of mass of the system is initially at a distance of 10 m above the floor, the distance of the man when the stone reaches the floor will be 10 + x = 10.1 m.

[You can apply the law of conservation of momentum and obtain the ‘recoil speed’ v of the man from the equation, 50×v = 0.5×2, from which v = 0.02 ms^–1.

The time taken by the stone to reach the floor is 10/2 = 5 s. During this time the man will move up through a distance 0.02×5 = 0.1 m so that when the stone reaches the floor, the man will be at a distance 10 + 0.1 = 10.1 m above the floor].

(2) Two particles which are initially at rest move towards each other under the action of their internal attraction. If their speeds are v and 2v at any instant, then the speed of centre of mass of the system will be

(1) v

(2) 2 v

(3) zero

(4) 1.5 v

Since the particles are initially at rest, the speed of the centre of mass of the system is zero. Since there are no external forces on the system, the centre of mass will continue to be at rest even though the particles are moving under the action of their internal attraction. Therefore the correct option is (3).

By trying a search for ‘centre of mass’ using the search box provided on this page, you can access all posts on centre of mass on this site.

You will find some additional posts on centre of mass at AP Physics Resources.

Solution to Multiple Choice Questions on Centre of Mass

Two multiple choice questions on centre of mass were given to you for practice yesterday. Here is the solution along with the questions:

(1) A boy weighing 40 kg is standing on a wooden log of mass 500 kg floating on still water in a lake. The distance of the boy from the shore is 12 m. The viscous force exerted by water on the wooden log may be neglected. If the boy walks slowly along the wooden log through 2 m towards the shore, the centre of mass of the system (wooden log and the boy) will move with respect to the shore through a distance

(a) 2 m (b) 1.25 m (c) 0.25 m (d) 0.16 m (e) zero

You should have worked this out within seconds. The centre of mass will be unaffected with respect to external fixed points if there are no external forces acting on the system. So, the correct option is (e).

(2) A T-shaped object with dimensions shown in the figure, is lying on a smooth floor. A force F is applied at the point P parallel to AB, such that the object has only translational motion without rotation. Find the location of P with respect to C

(a) L (b) 4L/3 (c) 3L/2 (d) 2L/3

The point P must be the centre of mass of the T-shaped object since the force F does not produce any rotational motion of the object. So, we have to find the distance of the centre of mass from the point C.

The horizontal part of the T-shaped object has length L. If the mass of the horizontal portion is ‘m’, the mass of the vertical portion of the T- shaped object is 2m since its length is 2L. For finding the centre of mass of the T shaped object, it is enough to consider two point masses m and 2m located respectively at the mid points of the horizontal and vertical portions of the T.

Therefore, the T-shaped object reduces to two point masses m and 2m at distances 2L and L respectively from the point C. The distance ‘r’ of the centre of mass of the system from the point C is given by

r = (m₁r₁ + m₂r₂)/(m₁ + m₂) = (m×2L + 2m×L)/(m + 2m) = 4L/3

[ Note that we have used the equation, r = (m₁r₁ + m₂r₂)/(m₁ + m₂) for the position vector r of the centre of mass in terms of the position vectors r₁ and r₂ of the point masses m₁ and m₂. We could use the simple equation involving the distances from C since the points are collinear].

Two Multiple Choice Questions on Centre of Mass (For practice)

Here are two questions on centre of mass. These are meant for checking whether you have a clear idea of the concept of centre of mass:

(1) A boy weighing 40 kg is standing on a wooden log of mass 500 kg floating on still water in a lake. The distance of the boy from the shore is 12 m. The viscous force exerted by water on the wooden log may be neglected. If the boy walks slowly along the wooden log through 2 m towards the shore, the centre of mass of the system (wooden log and the boy) will move with respect to the shore through a distance

(a) 2 m (b) 1.25 m (c) 0.25 m (d) 0.16 m (e) zero

(2) A T-shaped object with dimensions shown in the figure, is lying on a smooth floor. A force F is applied at the point P parallel to AB, such that the object has only translational motion without rotation. Find the location of P with respect to C

(a) L
(b) 4L/3
(c) 3L/2
(d) 2L/3

This MCQ appeared in AIEEE 2005 question paper.

Try to find the answer to the above questions. If you have clear understanding of the centre of mass, you will be able to find the answers in a couple of minutes. I’ll be back with the solution shortly.

An IIT-JEE 2007 Question on Centre of Mass

Here is an assertion-reason type MCQ (involving centre of mass motion) which appeared in IIT-JEE 2007 question paper:

STATEMENT-1

If there is no external torque on a body about its centre of mass, then the velocity of the centre of mass remains constant

because

STATEMENT-2

The linear momentum of an isolated system remains constant.

(a) Statement-1 is True, Statement-2 is True; Statement-2 is a correct

explanation for Statement-1

(b) Statement-1 is True, Statement-2 is True; Statement-2 is NOT a correct

explanation for Statement-1

(c) Statement-1 is True, Statement-2 is False

(d) Statement-1 is False, Statement-2 is True

This is a very simple question meant for checking your understanding of basic principles. But if you are not careful, you are liable to pick out a wrong answer!

Generally, if there are external torques or forces or both, the velocity of the centre of mass will change. So, the condition of no external torque alone is not sufficient to ensure the constancy of the velocity of the centre of mass. Statement-1 is therefore false.

[You should also note that an external torque about the centre of mass will not change the velocity of the centre of mass].

Statement-2 is evidently true.

The correct option therefore is (d).

Questions on Centre of Mass

The following question involving the motion of centre of mass is worth noting:

Two spheres of masses m₁ and m₂ (m₁>m₂) respectively are tied to the ends of a light, inextensible string which passes over a light frictionless pulley. When the masses are released from their initial state of rest, the acceleration of their centre of mass is
(a) [(m₁–m₂)/(m₁+m₂)]g
(b) [(m₁–m₂)/2(m₁+m₂)]g
(c) [(m₁–m₂)/4(m₁+m₂)]g
(d) [(m₁–m₂)/(m₁+m₂)]²g
(e) [4(m₁–m₂)/(m₁+m₂)]g
If r₁ and r₂ are the position vectors of the centres of the spheres, the position vector of their centre of mass is given by R = (m₁r₁ + m₂r₂)/(m₁+m₂). The acceleration of the centre of mass is therefore given by
a = d²R/dt² = (m₁d²r₁/dt² + m₂ d²r₂/dt²)/(m₁+m₂).
But d²r₁/dt² and d²r₂/dt², which are the accelerations of the masses m1 and m2 have the same magnitude (m₁–m₂)g/(m₁+m₂). If we take the acceleration of m₁ (which is downwards) as positive, that of m₂ is negative.
Therefore, a = [m₁(m₁–m₂)g/(m₁+m₂) – m₂(m₁–m₂)g/(m₁+m₂)] /(m₁+m₂).
On simplifying, this yields a = [(m₁–m₂)/(m₁+m₂)]²g. [Option (d)].
The following MCQ has been popular among question setters:
In the HCl molecule, the separation between the nuclei of the two atoms is about 1.27 Ǻ. The approximate distance of the centre of mass (from the hydrogen atom) of the HCl molecule, assuming the chlorine atom to be about 35.5 times as massive as the hydrogen atom is
(a) 0.27 Ǻ
(b) 0.56 Ǻ
(c) 1 Ǻ
(d) 1.24 Ǻ
(e) 2.26 Ǻ
The centre of mass of this two particle system is on the line joining the two atoms and in between these atoms. If ‘x’ is the distance of the centre of mass from the hydrogen atom, we have x = (1×0 + 35.5×1.27)/ (1+35.5) = 1.24 Ǻ, approximately.
Note that the equation giving the value of ‘x’ is the usual equation for the position vector of the centre of mass: R = (m₁r₁ + m₂r₂)/(m₁+m₂). We have taken the origin to be at the centre of the hydrogen atom so that r₁ = 0 and r₂ = 1.27 Ǻ.
[You can easily find the centre of mass of two particle systems by equating the ‘moments’ of the masses about the centre of mass. In the present case, 1×x = 35.5(1.27–x) from which x = 1.24 Ǻ].
Now consider the following simple question:
A proton and an electron, initially at rest, are allowed to move under their mutal attractive force. Their centre of mass will
(a) move towards the proton
(b) move towards the electron
(c) remain stationary
(d) move in an unpredictable manner.

The correct option is (c) because you require an external force to move the centre of mass of a system of particles. The mutual force of electrical attraction is an internal force which can not affect the position of the centre of mass of the system.