Two spheres of masses m1 and m2 (m1>m2) respectively are tied to the ends of a light, inextensible string which passes over a light frictionless pulley. When the masses are released from their initial state of rest, the acceleration of their centre of mass is
(a) [(m1–m2)/(m1+m2)]g
(b) [(m1–m2)/2(m1+m2)]g
(c) [(m1–m2)/4(m1+m2)]g
(d) [(m1–m2)/(m1+m2)]2g
(e) [4(m1–m2)/(m1+m2)]g
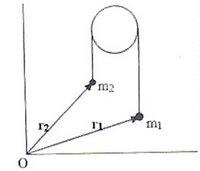
If r1 and r2 are the position vectors of the centres of the spheres, the position vector of their centre of mass is given by R = (m1r1 + m2r2)/(m1+m2). The acceleration of the centre of mass is therefore given by
a = d2R/dt2 = (m1d2r1/dt2 + m2 d2r2/dt2)/(m1+m2).
But d2r1/dt2 and d2r2/dt2, which are the accelerations of the masses m1 and m2 have the same magnitude (m1–m2)g/(m1+m2). If we take the acceleration of m1 (which is downwards) as positive, that of m2 is negative.
Therefore, a = [m1(m1–m2)g/(m1+m2) – m2(m1–m2)g/(m1+m2)] /(m1+m2).
On simplifying, this yields a = [(m1–m2)/(m1+m2)]2g. [Option (d)].
The following MCQ has been popular among question setters:
In the HCl molecule, the separation between the nuclei of the two atoms is about 1.27 Ǻ. The approximate distance of the centre of mass (from the hydrogen atom) of the HCl molecule, assuming the chlorine atom to be about 35.5 times as massive as the hydrogen atom is
(a) 0.27 Ǻ
(b) 0.56 Ǻ
(c) 1 Ǻ
(d) 1.24 Ǻ
(e) 2.26 Ǻ
The centre of mass of this two particle system is on the line joining the two atoms and in between these atoms. If ‘x’ is the distance of the centre of mass from the hydrogen atom, we have x = (1×0 + 35.5×1.27)/ (1+35.5) = 1.24 Ǻ, approximately.
Note that the equation giving the value of ‘x’ is the usual equation for the position vector of the centre of mass: R = (m1r1 + m2r2)/(m1+m2). We have taken the origin to be at the centre of the hydrogen atom so that r1 = 0 and r2 = 1.27 Ǻ.
[You can easily find the centre of mass of two particle systems by equating the ‘moments’ of the masses about the centre of mass. In the present case, 1×x = 35.5(1.27–x) from which x = 1.24 Ǻ].
Now consider the following simple question:
A proton and an electron, initially at rest, are allowed to move under their mutal attractive force. Their centre of mass will
(a) move towards the proton
(b) move towards the electron
(c) remain stationary
(d) move in an unpredictable manner.
(a) [(m1–m2)/(m1+m2)]g
(b) [(m1–m2)/2(m1+m2)]g
(c) [(m1–m2)/4(m1+m2)]g
(d) [(m1–m2)/(m1+m2)]2g
(e) [4(m1–m2)/(m1+m2)]g
If r1 and r2 are the position vectors of the centres of the spheres, the position vector of their centre of mass is given by R = (m1r1 + m2r2)/(m1+m2). The acceleration of the centre of mass is therefore given by
a = d2R/dt2 = (m1d2r1/dt2 + m2 d2r2/dt2)/(m1+m2).
But d2r1/dt2 and d2r2/dt2, which are the accelerations of the masses m1 and m2 have the same magnitude (m1–m2)g/(m1+m2). If we take the acceleration of m1 (which is downwards) as positive, that of m2 is negative.
Therefore, a = [m1(m1–m2)g/(m1+m2) – m2(m1–m2)g/(m1+m2)] /(m1+m2).
On simplifying, this yields a = [(m1–m2)/(m1+m2)]2g. [Option (d)].
The following MCQ has been popular among question setters:
In the HCl molecule, the separation between the nuclei of the two atoms is about 1.27 Ǻ. The approximate distance of the centre of mass (from the hydrogen atom) of the HCl molecule, assuming the chlorine atom to be about 35.5 times as massive as the hydrogen atom is
(a) 0.27 Ǻ
(b) 0.56 Ǻ
(c) 1 Ǻ
(d) 1.24 Ǻ
(e) 2.26 Ǻ
The centre of mass of this two particle system is on the line joining the two atoms and in between these atoms. If ‘x’ is the distance of the centre of mass from the hydrogen atom, we have x = (1×0 + 35.5×1.27)/ (1+35.5) = 1.24 Ǻ, approximately.
Note that the equation giving the value of ‘x’ is the usual equation for the position vector of the centre of mass: R = (m1r1 + m2r2)/(m1+m2). We have taken the origin to be at the centre of the hydrogen atom so that r1 = 0 and r2 = 1.27 Ǻ.
[You can easily find the centre of mass of two particle systems by equating the ‘moments’ of the masses about the centre of mass. In the present case, 1×x = 35.5(1.27–x) from which x = 1.24 Ǻ].
Now consider the following simple question:
A proton and an electron, initially at rest, are allowed to move under their mutal attractive force. Their centre of mass will
(a) move towards the proton
(b) move towards the electron
(c) remain stationary
(d) move in an unpredictable manner.
The correct option is (c) because you require an external force to move the centre of mass of a system of particles. The mutual force of electrical attraction is an internal force which can not affect the position of the centre of mass of the system.
Whoa! This blog looks exactly like my old one!
ReplyDeleteIt's on a entirely different topic but iit has pretty much the same page layout and design. Outstanding choice of colors!
Feel free to visit my weblog :: adidas duffle bag kohl's