Two more Questions on Spherical Mirrors

The following question is quite simple, but many among you will find it confusing:
The sun subtends an angle of 0.5° on the earth’s surface. What is the diameter of the image of the sun, produced by a concave mirror of radius of curvature one metre?(a) 8.8mm (b) 6.4mm (c) 5mm (d) 4.4mm (e) data insufficient for arriving at an answer
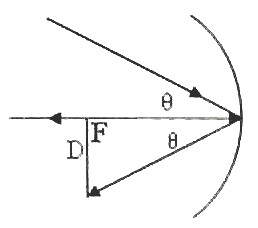
In the figure θ is the angle subtended by the sun at the pole of the mirror. The real image of the sun is obtained at the focus of the mirror and this image also subtends the same angle θ at the pole of the mirror. Since the real image of the sun is obtained at the focus of the mirror, we have D/50 = 0.5×π/180 where D is the diameter of the image of the sun. [Note that the focal length of the mirror is 50cm and we have converted the angle of 0.5° in to radian].
From the above equation we obtain D = 0.44 cm (approximately) = 4.4mm.
The following question also is simple, but be careful while applying the signs in accordance with the Cartesian convention.
An erect image three times the size of a real object is formed with a concave mirror of radius of curvature 36cm. The distance of the object from the mirror is
(a) 24cm (b) 20cm (c) 16cm (d) 12cm (e) 8cm
Evidently, the signs of ‘f’ and ‘u’ are negative. Since the image is erect, it must be formed behind the mirror (virtual image) and the sign of ‘v’ is positive. Further, the image is magnified 3 times so that v=3u. Substituting these in the equation, 1/f = 1/u + 1/v, we have –1/18 = –1/u +1/3u from which u =12 cm.