Charges +q, +q, –q and –q coulomb are arranged at the corners of an imaginary rectangle of sides 6m and 4m, as shown in the adjoining figure. A and B are the mid points of the longer sides. The potential difference between A and B is (in volts)
(a) 2.4×106q (b) 4.8×106q (c) 2.4×109q (d) 4.8×109q (e)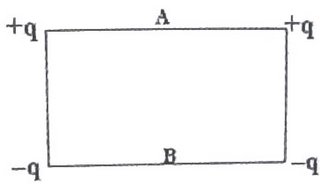
9.6×109q
(a) 2.4×106q (b) 4.8×106q (c) 2.4×109q (d) 4.8×109q (e)
9.6×109qThe potential at A due to the charges +q and +q is 2×(1/4πε0)(q/3) and the potential at the same point due to the charges –q and –q is 2×(1/4πε0))(–q/5). The resultant potential at A is 2×(1/4πε0)[(q/3)–(q/5)] = 2×(1/4πε0) (2q/15)= (1/4πε0) (4q/15).
Similarly, the resultant potential at B is 2×(1/4πε0)[(q/5) – (q/3)] =
Similarly, the resultant potential at B is 2×(1/4πε0)[(q/5) – (q/3)] =
2×(1/4πε0) (–2q/15) = (1/4πε0)(–4q/15).
The potential difference between points A and B is (1/4πε0))[(4q/15) – (–4q/15)] = (1/4πε0)×(8q/15). You should remember that 1/4πε0= 9×109. Therefore, the P.D. is 9×109×(8/15)q = 4.8×109q volts.
The following question appeared in Punjab CEET 2003 question paper:
As shown in figure, if the point C is earthed and the point A is given a potential of 2000 volt, then the potential at B will be
The potential difference between points A and B is (1/4πε0))[(4q/15) – (–4q/15)] = (1/4πε0)×(8q/15). You should remember that 1/4πε0= 9×109. Therefore, the P.D. is 9×109×(8/15)q = 4.8×109q volts.
The following question appeared in Punjab CEET 2003 question paper:
As shown in figure, if the point C is earthed and the point A is given a potential of 2000 volt, then the potential at B will be
(a) 400 V (b) 500 V (c) 1000 V (d) 1300 V
The effective capacitance between the points B and C is 15 μF because 10μF and 10μF in series in the upper branch make 5μF and this is in parallel with 10μF in the lower branch. So, in effect 2000 V is applied across the series combination of 5μF and 15μF connected between A and C. Since the potential difference across capacitors connected in series is inversely proportional to the capacitance, the applied P.D. of 2000 volts get divided in the ratio 3: 1 across 5μF and 15μF [1500 V : 500V]. The potential at B with respect to the grounded point C is therefore 500V.
The effective capacitance between the points B and C is 15 μF because 10μF and 10μF in series in the upper branch make 5μF and this is in parallel with 10μF in the lower branch. So, in effect 2000 V is applied across the series combination of 5μF and 15μF connected between A and C. Since the potential difference across capacitors connected in series is inversely proportional to the capacitance, the applied P.D. of 2000 volts get divided in the ratio 3: 1 across 5μF and 15μF [1500 V : 500V]. The potential at B with respect to the grounded point C is therefore 500V.
Now consider the following question which appeared in IIT 2002 question paper:
Two identical capacitors have the same capacitance C. One of them is charged to potential V1 and the other to potential V2. The negative ends of the capacitors are connected together. When the positive ends are also connected, the decrease in energy of the combined system is
(a) ¼ C(V12 – V22) (b) ¼ C(V12 + V22) (c) ¼ C(V1 – V2)2 (d) ¼ C(V1 + V2)2
The initial energy of the system is ½ CV12 + ½ CV22 = ½ C(V12+V22).
On connecting the capacitors (in parallel), the net capacitance of the system is 2C and the net voltage across the combination is ½ (V1+V2). [The total charge is C(V1+V2) so that the net voltage is C(V1+V2)/ 2C = (V1+V2)/2].
Therefore, final energy of the system is(½) × 2C[(V1+V2)/2]2 = ¼ C(V12+V22 +2V1V2).
On subtracting the final energy from the initial energy, we obtain the decrease in energy as ¼ C(V1–V2)2, given by option (c).
Two identical capacitors have the same capacitance C. One of them is charged to potential V1 and the other to potential V2. The negative ends of the capacitors are connected together. When the positive ends are also connected, the decrease in energy of the combined system is
(a) ¼ C(V12 – V22) (b) ¼ C(V12 + V22) (c) ¼ C(V1 – V2)2 (d) ¼ C(V1 + V2)2
The initial energy of the system is ½ CV12 + ½ CV22 = ½ C(V12+V22).
On connecting the capacitors (in parallel), the net capacitance of the system is 2C and the net voltage across the combination is ½ (V1+V2). [The total charge is C(V1+V2) so that the net voltage is C(V1+V2)/ 2C = (V1+V2)/2].
Therefore, final energy of the system is(½) × 2C[(V1+V2)/2]2 = ¼ C(V12+V22 +2V1V2).
On subtracting the final energy from the initial energy, we obtain the decrease in energy as ¼ C(V1–V2)2, given by option (c).
You will find more multiple choice questions on Electrostatics with solution in the post dated 9th October 2006.
No comments:
Post a Comment