More Multiple Choice Questions on Rotational Motion & Moment of Inertia

Here is an interesting question which appeared in

Kerala Engineering Entrance - 2006 test paper

( and also in IIT screening 2000 question paper):

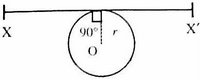
A thin wire of length ‘L’ and uniform linear mass density ρ is bent into a circular loop with centre at O and radius ‘r’ as shown. The moment of inertia of the loop about the axis XX’ is
(a) 3ρL³/8π² (b) ρL³/16π² (c) 3ρL³/8π²r (d) ρL³/8π²r (e) 3ρL³/16π²

The moment of inertia of a circular ring about a diameter is ½ mr², with usual notations. The axis of rotation in the question is a tangent to the ring. The moment of inertia of the ring about the tangent is ½ mr² + mr² = (3/2)mr², on applying the parallel axis theorem. Now, m= ρL and the radius ‘r’ is given by 2πr = L, from which r = L/2π
On substituting for ‘m’ and ‘r’, moment of inertia = (3/2) Lρ×L²/ 4π² = 3ρL³/8π², given in option(a).
The following simple question appeared in Kerala Medical Entrance 2006 test paper:
Moment of inertia of a body does not depend upon its
(a) mass (b) axis of rotation (c) shape (d) distribution of mass (e) angular velocity
The correct option, as you might be knowing, is (e). Occasional simple questions like this will help you in saving your time for spending on other difficult questions. Good question setters will usually include a few simple questions for boosting your morale!
The following MCQ which also appeared in Kerala Medical Entrance 2006 test paper is worth noting:
A solid cylinder rolls down an inclined plane of height 3m and reaches the bottom of the plane with angular velocity of 2√2 rad.s-1. The radius of the cylinder must be
(a) 5 cm (b) 0.5 m (c) √10 m (d) √5 m (e) 10 cm
The initial gravitational potential energy (Mgh) of the cylinder is converted to rotational and translational kinetic energy when the cylinder reaches the bottom of the plane so that we can write,
Mgh = ½ Iω² + ½ Mv² where M is the mass, ‘v’ is the linear velocity, I is the moment of inertia and ‘ω’ is the angular velocity of the cylinder.
Since v = ωR and I = ½ MR², the above equation becomes
Mgh = ½ ×(½ MR²) ω² + ½ Mω²R², which yields R = √[4gh/3ω²] = √5, on substituting for g,h and ω.
Now see whether you can solve the following problem in a minute:

A solid sphere rolls (without slipping) down a plane inclined at 30˚ to the horizontal. The distance traveled in √7 seconds after starting from rest is (g = 10 ms^-2)
(a) 5.5 m (b) 6.25 m (c) 12.5 m (d) 15 m (e) 17.5 m
If you remember that the acceleration of a body rolling down an incline of angle θ is (gsinθ)/[1+ (k²/R²), where ‘k’ is the radius of gyration and R is the radius of the rolling body, you will be able to solve this in one minute. The radius of gyration of a solid sphere about its diameter is (2/5)R² since its moment of inertia, I = (2/5)MR², which can be equated to Mk². Therefore, k²/R² = 2/5 for a solid sphere. Its acceleration = (g sin30˚)/[1+(2/5)] = (10×½)/(7/5) = 25/ 7.
We have s = ut + ½ at² = 0 + ½ ×(25/7) ×7 = 12.5 m [Option (c)].

You will find more multiple choice questions (with solution) on rotational motion here.